2차원 누적합으로 2차원 배열을 풀어보자.
2차원 배열의 누적합도 1차원 배열의 누적합과 크게 다르지 않다. 1차원 배열에서 sum[N]은 1번째부터 N번째까지의 합을 나타냈다. 그럼 이차원 배열 sum[N][M]을 (0,0)부터 (N,M)까지의 합이라고 해보자.
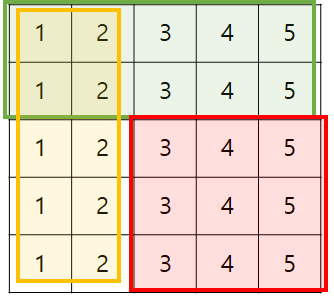
빨간 부분 (3, 3)부터 (5, 5)의 합을 어떻게 구할 수 있을까?
prefixSum[5][5]는 (1,1)부터 (5,5)까지의 합을 나타내므로 해당 부분에서
녹색 부분(prefixSum[2][5])을 빼주고,
노란 부분(prefixSum[5][2])을 빼주고,
두 번 빠진 녹색과 노란색이 만나는 부분(prefixSum[2][2])를 한번 더 더해주면 될 것이다.

그럼 (0,0)부터 (N,M)까지의 모든 위치의 값만 유효한 시간 내에 구할 수 있다면 그 이후 구간합은 O(1)의 시간복잡도로 구할 수 있게 된다.
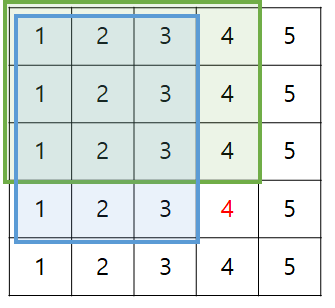
그럼 (1,1)부터 (x, y)까지의 합은 어떻게 구할까?
입력으로 들어온 값인 arr[][] 그림을 보자. 저기서 빨간 글자 부분(4,4)에 해당하는 prefixSum[4][4]는 prefixSum[4-1][4] + prefixSum[4][4-1] - prefixSum[4-1][4-1] + arr[4][4]로 구할 수 있다. 즉, 녹색 부분과 파란 부분의 누적합을 더하고, 겹치는 부분은 두 번 더해졌으므로 한번 빼주고, 현재 값을 더해주면 된다.
RxC 크기의 배열을 입력받았을 때를 기준으로 코드는 다음과 같다.
for (int i = 1; i <= R; i++) {
for (int j = 1; j <= C; j++) {
prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + arr[i][j];
}
}
마찬가지로 prefixSum 배열을 추가로 만들지 않고, 기존 arr 배열의 값이 이후 필요가 없다면 arr에 바로 만들어도 된다.
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
arr[i][j] += arr[i-1][j] + arr[i][j-1] - arr[i-1][j-1];
}
}
arr에서 바로 prefix sum을 구하는 과정을 보자. 파란선 A->B은 B+=A를 뜻한다. 주황선 A->B는 B-=A를 뜻한다.


그럼 이제 원하는 2차원 누적합을 O(1)에 구해볼 수 있다! 예를 들어 (2,2)부터 (5,3)의 구간합을 구해보자. 좌측 arr 배열에서 직접 구하려면 2+3+2+3+2+3+2+3 = 20이다. 우측 prefixSum에서 구하려면 30-6-5+1 = 20이다.

최종적으로 시간복잡도는 다음과 같다.
A. 2차원 구간의 합을 직접 for문을 돌려 구하는 경우 = O(RC+QRC)
B. 1차원 누적합을 각 행마다 계산하는 경우 = O(RC+QR)
C. 2차원 누적합 사용 = O(RC+Q)
입력받으면서 바로 prefixSum도 만들 수 있으므로 셋에 동일하게 존재하는 O(RC) 부분을 제외하면 O(QRC)에서 O(Q)로 줄어든 셈이다.
2차원 누적합의 가장 대표적인 문제다.
백준 11660 구간 합 구하기5
https://www.acmicpc.net/problem/11660
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
/*
표의 크기 N, 합을 구해야하는 횟수 M
*/
int N, M;
int arr[1025][1025];
int prefixSum[1025][1025];
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> N >> M;
for(int i = 1; i <= N; i++){
for(int j= 1; j <= N; j++){
cin >> arr[i][j];
prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1] + arr[i][j];
}
}
while(M--){
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << prefixSum[x2][y2] - prefixSum[x1 - 1][y2] - prefixSum[x2][y1 - 1] + prefixSum[x1 - 1][y1 - 1] << "\n";
}
return 0;
}'🍞 Algorithm' 카테고리의 다른 글
| [백준] 17406 배열 돌리기4 java (0) | 2025.01.20 |
|---|---|
| [Algorithm] DP 배낭 채우기 (Knapsack) (0) | 2024.10.22 |
| [Softeer] Softeer 출퇴근길 c++ (0) | 2024.09.03 |
| [Algorithm] 누적합(Prefix sum)을 이용한 구간합 구하기 (0) | 2023.06.28 |