도둑이 보석가게에 배낭을 메고 침입했다.
배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 찢어질 것이다.
각 보석들의 무게와 가격은 알고 있다.
배낭이 찢어지지 않는 선에서 가격 합이 최대가 되도록 보석을 담는 방법은?
배낭 채우기 문제는 다이나믹 프로그래밍의 유명한 유형이다.
그중에서도 보석을 자를 수 있다고 가정하는 Fractional Knapsack 문제와
자를 수 없다고 가정하는 0-1 Knapsack 문제가 있는데,
전자보다는 후자가 주로 다루어진다.
0-1 Knapsack 문제는 다이나믹 프로그래밍이라는 방법을 쓰는 기본적인 문제로 알려져 있다.
DP를 잘 모른다면 생각나는 방법은 두 가지 정도가 있을 것이다.
1. 모든 경우의 수를 넣어본다 (Brute-Force)
n개의 보석이 있다고 치면, n개 보석으로 만들 수 있는 가능한 부분집합의 수는 2^n개다. 최악의 경우에는 2^n번까지 봐야 하는, 즉 O(2^n)의 알고리즘은 너무 느리다.
2. 가격이 높은 보석, 혹은 (가격/무게)의 값이 제일 높은 보석부터 먼저 골라서 넣는다. (Greedy)
아래의 그림을 보자. 가격이 제일 높은 보석을 먼저 고르는 방법을 쓴다고 하면, 오른쪽 아래에 있는 빨간 보석을 먼저 고르고 그다음 왼쪽에 있는 노란 보석을 고를 것이다. 그러면 10kg가 차고 가격의 합은 $16이 된다.
그렇지만 그림을 잘 보면서 다른 방법을 찾아보면, 왼쪽 보석 3개를 넣으면 10kg에 $17이 된다는 걸 쉽게 알 수 있고, 1/2/3/4kg짜리를 하나씩 조합해서 넣으면 $19까지도 나온다. 즉 이 방법은 최적의 답을 보장하지 못한다.

단순히 가격만 보지 말고, '무게당 가격'을 계산해서 제일 높은 것부터 넣으면 되지 않겠느냐고 생각할 수 있다. 실제로 위 그림의 예시에서는 그렇게 하면 최적의 답이 나오긴 한다. 하지만 언제나 그렇지는 않다.
W=30kg
보석1: 5kg/$5 -- kg당 $1
보석2: 10kg/$6 -- kg당 $0.6
보석3: 20kg/$14 -- kg당 $0.7
이 경우에 '무게당 가격' 순으로 보석을 넣으면 보석 1, 보석 3이 들어가며 가격의 합은 $19이다. 그런데 배낭 무게가 5kg가 남는다. 보석 2를 넣을 수는 없으므로 5kg는 그냥 쓸데없이 남는 공간이다. 보석 2, 보석 3을 넣으면 30kg가 꽉 차고 가격의 합이 $20이다. 도둑 입장에서 도망갈 때 배낭이 좀 더 무거울 수 있겠지만 어쨌든 문제의 조건은 배낭이 안 터지는 한도 내에서 가격 합을 최대화하는 것이므로 보석 2,3을 가져가는 것이 정답이다.
이처럼 특정한 기준을 정해놓고 그 기준의 값이 가장 높은 순으로 집는 걸 Greedy 알고리즘이라고 하는데 0-1 배낭 채우기 문제는 Greedy 한 방법으로는 풀 수 없는 문제다.
+ Fractional Knapsack(보석을 자를 수 있는) 문제는 Greedy로 풀 수 있다. 위 예시에서 보석 2를 반으로 잘라서 남은 5kg짜리 공간에 넣으면 그게 최적의 답이 된다.
그래서 DP라는 게 등장한다. DP는 큰 문제를 작은 문제로 쪼개서 해결한다라는 원리에 기반을 두고 있으며, 이전에 계산해 둔 값을 메모리에 저장해서 반복 작업을 줄이는 기법(Memoization)이 핵심이다.
DP를 0-1 배낭 채우기 문제를 푸는데 적용해보자. 어떤 문제를 DP로 풀기 위해서는 '최적의 원리'가 성립하는지를 확인해야 하는데, 최적의 원리란 다음과 같다.
어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함하고 있으면, 그 문제에 대하여 최적의 원리가 성립한다.
이 문제에서 이 원리가 성립할까? 집합 A를 n개의 보석들 중에 최적으로 고른 부분집합이라고 가정하자.
- 집합 A가 n번째 보석을 포함하고 있지 않다면, A는 n번째 보석을 뺀 나머지 n-1개의 보석들 중에서 최적으로 고른 부분집합과 같다.
- 집합 A가 n번째 보석을 포함하고 있다면, A에 속한 보석들의 총가격은 n-1개의 보석들 중에서 최적으로 고른 가격의 합에다가 보석 n의 가격을 더한 것과 같다. (단, n번째 보석을 넣었을 때 배낭이 터지지 않아야 한다.)
점화식으로 풀어보면 아래와 같다.
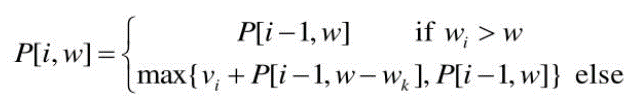
P[i, w]란 i개의 보석이 있고 배낭의 무게 한도가 w일 때 최적의 이익을 의미한다.
- i번째 보석이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 보석을 뺀 i-1개의 보석들을 가지고 구한 전 단계의 최적값을 그대로 가져온다.
- 그렇지 않은 경우, i번째 보석을 위해 i번째 보석만큼의 무게를 비웠을 때 최적값에 i번째 보석의 가격을 더한 값 or i-1개의 보석들을 가지고 구한 전 단계의 최적값 중 큰 것을 선택한다.
P라는 2차원 리스트를 채워나가면서, 필요한 경우 "앞에서 계산했던 다른 칸의 값을 이용해서" 다음 값을 계산한다.

일단 i가 0인 경우는 넣을 보석이 없는 것이므로 다 0이고, w가 0인 경우에는 배낭이 없는 것이므로 다 0이다. 그래서 첫 번째 행과 첫번째 열은 다 0으로 채워 넣고 시작한다.

i=1인 경우부터 보자면, (i, w)가
(1, 1)인 경우에는 w=1짜리 배낭으로는 아무 보석도 넣을 수 없으므로 0이다.
(1, 2)인 경우에는 이제 1번 보석을 넣을 수 있으니까 V[1, 2] = 3이 된다.
직관적으로는 이렇고, 위의 식을 통해서 보면 '1번 보석의 가치 + V[0, 0]'의 값과 V[0, 2]의 값을 비교해서 더 큰 쪽을 가져가게 되는데, 1번 보석의 가치는 3이고 V[0, 0]과 V[0, 2]는 둘 다 0이므로 전자를 선택하게 된다.
현재 i=1이므로 1번 보석을 넣고 나면 더 이상 넣을 게 없으니 오른쪽의 남은 칸들도 다 3일 것이다.

i=2인 경우를 보면, w=2일 때는 현재 보고 있는 2번 보석(3kg)을 넣을 수 없으므로 바로 위칸의 3을 가져온다. (1번 보석을 넣는다.) w=3이 되면 2번 보석을 넣을 수 있게 되는데, 1번 보석을 넣었을 때(바로 위칸)랑 2번 보석을 넣을 만큼의 공간을 확보하고 2번 보석을 넣었을 때 (2번 보석의 가치 + V[1,0])를 비교해서 더 가치가 높은 쪽을 선택한다. 그래서 4가 들어간다.

(i, w)가 (2,5)이니 경우는 1번 보석과 2번 보석을 둘 다 넣을 수 있다. 이미 3이 들어있는 (1,2)에서 최적값을 가져온다는 것이 1번 보석을 빼지 않고도 2번 보석을 넣을 수 있음을 의미한다. 즉 1번 보석을 넣었던 칸의 최적값(3) + 2번 보석의 가격 = 7이 들어간다.

이런 식으로 나머지 칸들도 계산해 보면 마지막 칸에는 결국 7이 들어가고, 이 마지막 칸이 최종적인 답(최적의 총 가격)이 된다.
아래는 이를 C++ 함수로 구현한 것이다. DP를 위한 2차원 리스트를 만든 다음, 0번째 행/열을 0으로 세팅하고 나면 나머지는 위의 점화식을 그대로 프로그램으로 옮기면 된다. 백준의 배낭 대표 문제다. (평범한 배낭 12865번 골드5)
#include <iostream>
#include <algorithm>
using namespace std;
int N, K; // 물품의 수, 버틸 수 있는 무게
int W[101], V[101]; // 각 물건의 무게, 가치
int dp[101][100001];
void knapsack() {
for(int i = 1; i <= N; i++){
for(int j = 1; j <= K; j++){
// 담을 수 있는 경우
if (j >= W[i])
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);
// 담을 수 없는 경우
else dp[i][j] = dp[i - 1][j];
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
cin >> N >> K;
for(int i = 1; i <= N; i++){
cin >> W[i] >> V[i];
}
knapsack();
cout << dp[N][K];
return 0;
}https://www.acmicpc.net/problem/12865
'🍞 Algorithm' 카테고리의 다른 글
| [백준] 17406 배열 돌리기4 java (0) | 2025.01.20 |
|---|---|
| [Algorithm] 2차원 누적합 (0) | 2024.10.23 |
| [Softeer] Softeer 출퇴근길 c++ (0) | 2024.09.03 |
| [Algorithm] 누적합(Prefix sum)을 이용한 구간합 구하기 (0) | 2023.06.28 |